VSEPR - operachem

Estimated reading time: 9 minutes

Introduction
Spatial disposition of electrons
Lone pairs and bond pairs
Spatial disposition vs molecular geometry
How to determine molecular geometry
Recapitulatory table
Bond angles in VSEPR

Introduction

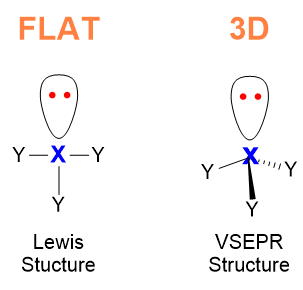
With this model, we are going to move from the flat and boring world of Lewis’s structures to the wide and geometric world of 3D (Figure 1).

Once learnt how to draw bonds and lone pairs around an atom by using Lewis model, the curious student might wonder : << Is there a 3D structure of molecules? Are molecules flat as Lewis taught, or do they have a 3D structure? >>.

You will find the answer to this question in this article. However, let’s start from the beginning: what does VSEPR mean?

VSEPR stands for valence shell electron pairs repulsion.

From the first two light blue words, we learn the first important concept of this model: VSEPR takes into account the valence electrons of the central atom in the molecule (even if central atom is implied in the acronym). The remaining violet words tell us that the model finds the three-dimensional structure of the molecule by considering the electron pairs repulsion around the central atom.

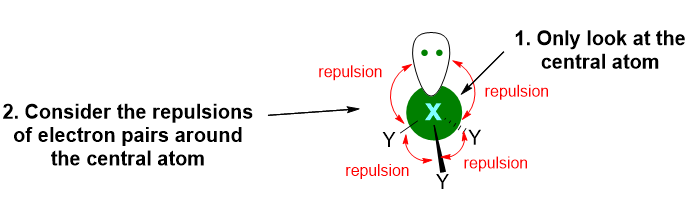
In other words, this model finds the 3D structure of molecules looking to the valence electron pairs of the only central atom and assuming that those pairs, since they are negatively charged, will tend to repels each other and to spatially organise as far away from each other as possible (Figure 2).

Would you like to have our flowchart, which sum up all the rules and you can bring everywhere? You can find it at page 9 of our pdf or docx files, you find here.

Spatial disposition of electrons

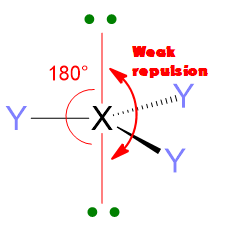
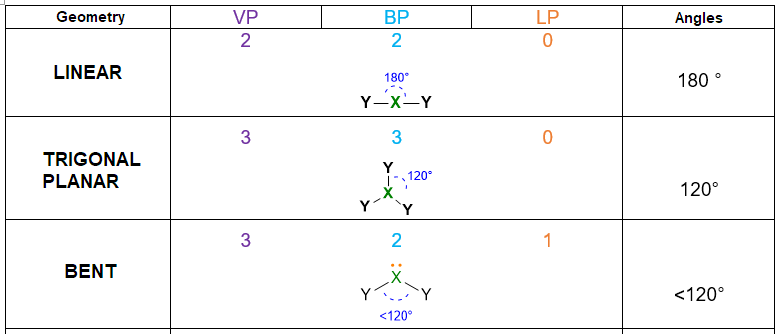
Therefore, repulsions between these valence pairs determine the shape of the molecule. Let’s take an example, if we have only 2 pairs of electrons around the central atom, regardless if they are bonding or lone pairs, these pairs will set in a way to stay as far away from each other as possible. Hence, they will place at 180° one from each other. As consequence, the spatial disposition of these two pairs will be linear.

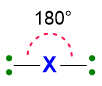
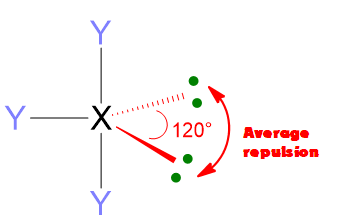
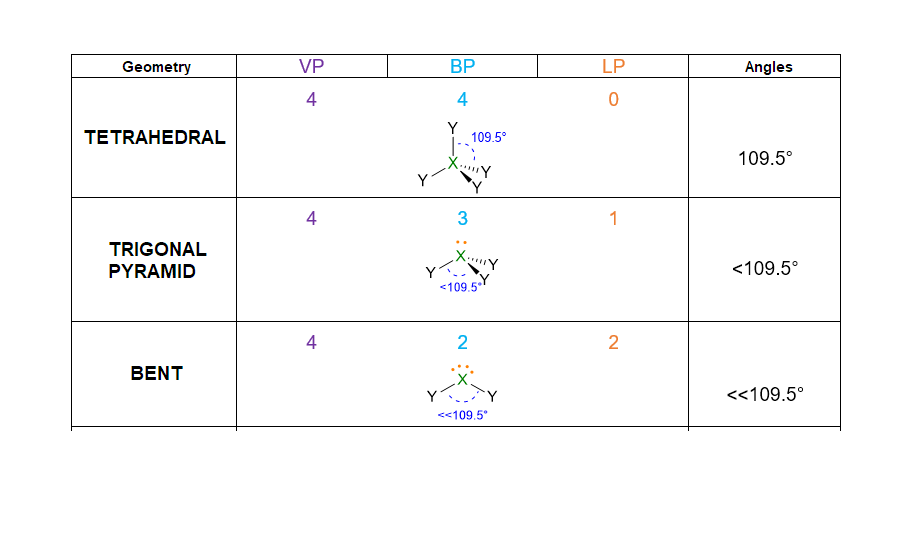
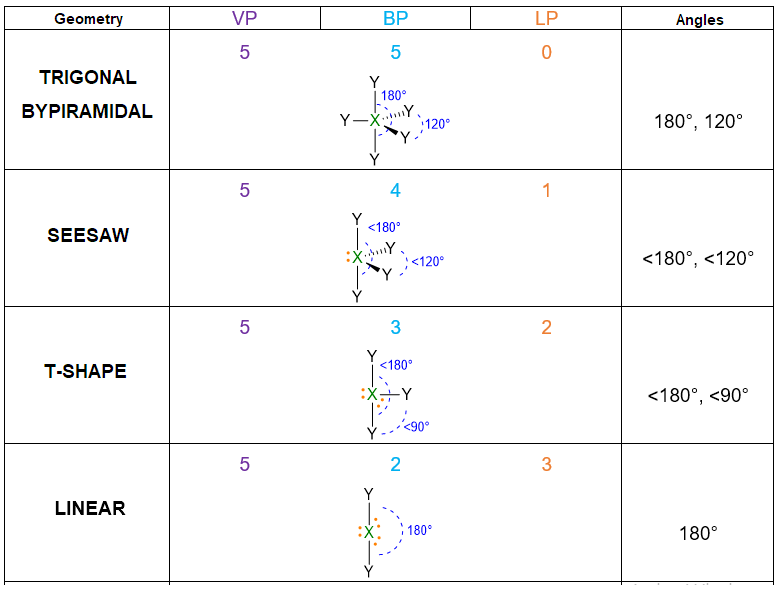
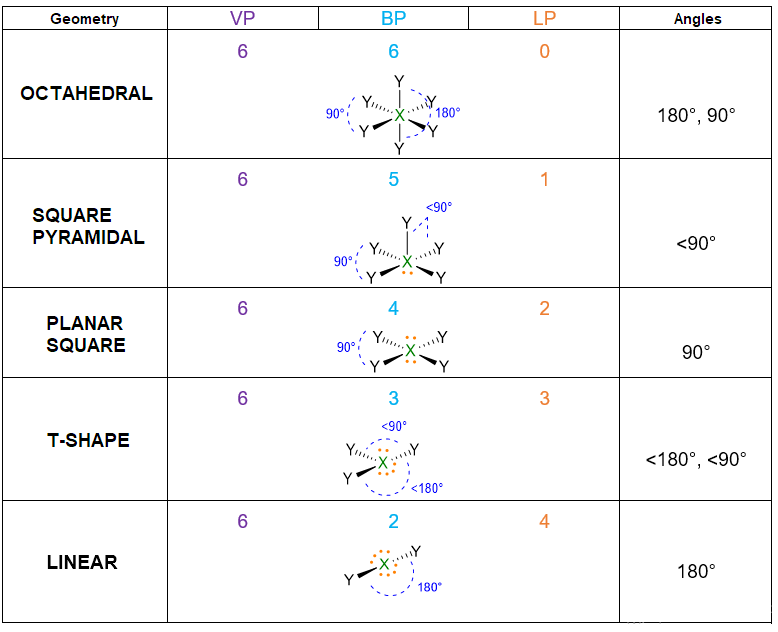
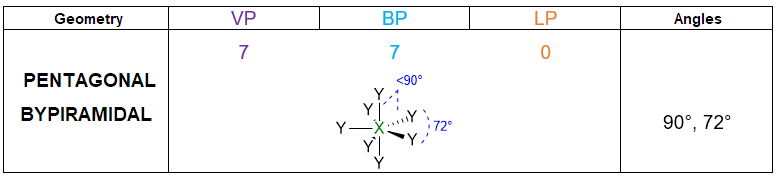
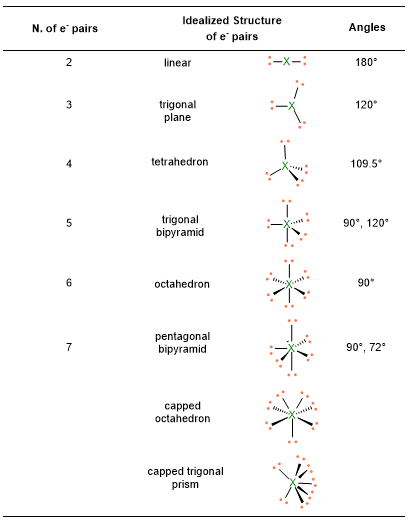
`Figura 3 - Spatial disposition of 2 electrons`

According to the numbers of electron pairs we have around the central atom, different spatial dispositions are possible. Table 1 summarizes all the cases from 2 to 7 pairs. For instance, 3 electron pairs will place at 120° away one from each other, forming a trigonal plane. On the other hand, 4 pairs will locate at 109.5° distant, giving rise to tetrahedron. Pairs from 5 to 6, will assume the disposition of trigonal bipyramid and octahedron respectively. However, in the case of 7 pairs, more than one dispositions is possible.

`Table 1 - Spatial disposition of electrons`

Lone pairs and bond pairs

So far, in this article, we have considered the electron pairs in general; however electron pairs consist of lone pairs and bond pairs.

In VSEPR model, the lone pairs are considered more spatially expanded than bond pairs. The reason of this lies in the fact that lone pairs move under the effective nuclear charge of only one atom, whereas bond pairs are affected by the nuclear charges of two atoms (Figure 4).

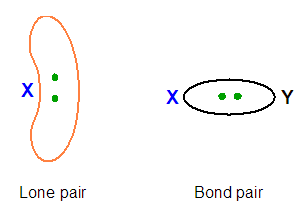
This difference between lone pairs and bond pairs can also be seen in the different electron density near the valence core. Particularly, lone pair contributes with two net negative charges around the central atom, while bond pair which shares its two electrons with two nuclei, provides a net electron density less than two electrons. The consequence of this is the following order of repulsion between electron pairs:

`Figure 5 - Order of repulsions of electron pairs`

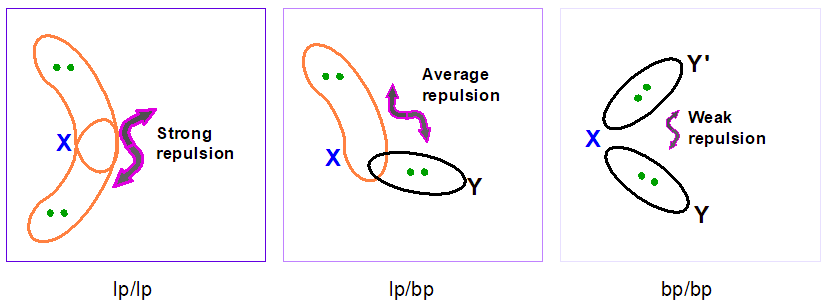
Therefore, two lone pairs (lp/lp) repel each other with a bigger strength than one lone pair and one bond pair (lp/bp). The weakest repulsion is between two bond pairs (bp/bp).

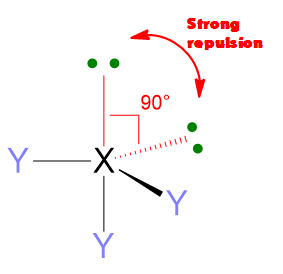
Another important feature of the electron pair repulsions is that they depend upon the angular distance of electron pairs. 2 electron pairs at 90° apart will repel much more than 2 pairs at 120° or even more if compared with pairs at 180°. Hence, the repulsions at 90° are the most important one to determine the molecular geometry.

Spatial disposition vs molecular geometry

Before continuing with VSEPR model, it is important to distinguish between the word spatial arrangement of electrons and molecular geometry:

The spatial arrangement of electrons indicates the position of electrons around the central atom; this property cannot be experimentally determined.
The molecular geometry indicates the spatial position of the nuclei in a molecule; this property can be experimentally determined.

An example, for spatial disposition of electrons has been shown in the previous table (Table 1), while the concept of molecular geometry will be discussed below.

How to determine molecular geometry

After this introduction, how can we extract the molecular geometry with VSEPR?

Just follow the directions below.

Write the Lewis structure of the molecule.
Count the number of lone pairs and bond pairs of the only central atom in the Lewis structure. The following equation can help you:

VP = BP + LP

Where VP = valence pairs;

BP = bond pairs;

LP = lone pairs.

Once you know the VP number, you can find the spatial disposition of electrons following the Table 1. E.g. VP = 4, the spatial disposition of electrons is tetrahedral, with angles of 109.5°.
If the molecule has LP = 0, then the spatial disposition is equivalent to the molecular geometry. In this case, you have already determined the geometry and you can stop here.
If the molecule has LP = 1 but VP < 5, then the molecular geometry is defined by the spatial disposition given in Table 1 but you need to erase the lone pairs (LP) and consider only the remaining bond pairs (BP) (see example below). If the molecule has LP = 1, but VP ≥ 5, you need again to start from the spatial disposition given by Table 1, however, this time you have first to find the most stable position for the lone pair (if placing it in axial position or in the equatorial one). The LP position should be selected in a way to minimize the repulsion lp/bp at 90°. Once found the most stable structure, erase the lone pair to find the molecular geometry/bp. (See example below).

Note: Lone pairs have never to be considered in the molecular geometry, since the geometry is always defined only by the position of the nuclei in the molecule. Indeed, when you define a molecular geometry, always erase the lone pairs at the end of the process and keep only the bond pairs.

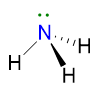
Let us see an example to understand points from 1 to 5. The NH₃ molecule has the following Lewis structure (point 1), from which we can extract VP, BP and LP of the central atom (point 2).

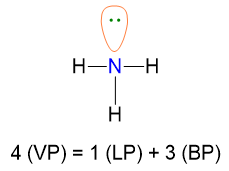
Since VP = 4, the spatial disposition is tetrahedral (point 3).

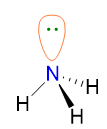
However, NH₃ has LP = 1, therefore its geometry is determined by erasing the lone pairs and considering the remaining 3 BP (point 5); as a result the NH₃ geometry is pyramidal.

ammonia piramide — `Pyramidal geometry of ammonia`

ammonia-animata1 — `Ammonia in the 3D space`

Let us do another example to understand the point 5 in the case of LP = 1 and VP ≥ 5. Let’s take the molecule of SF₅ as example. Its Lewis structure is the following:

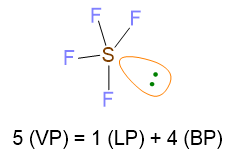
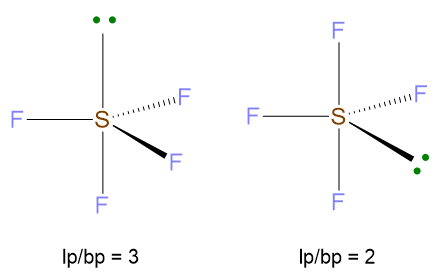
VP = 5, hence the spatial disposition of valence electrons is the trigonal bipyramid. On the other hand, since LP = 1 with VP ≥ 5, there is the issue where to place the lone pair, if in equatorial or axial position of the trigonal bipyramid. Therefore, all the possibilities must be evaluated and the disposition with the least repulsions lp/bp at 90° has to be chosen. In the figure below, you can see that lone pair in axial position gives rise to 3 repulsions lp/bp at 90°, while the lone pair in equatorial compromises only 2 repulsions lp/bp at 90°. In this last case, there are also 2 repulsions at 120°, but they are of lower entity because the angle is bigger than 90°. To conclude, the most stable structure is the second one.

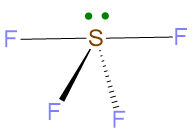
The geometry is determined by the only 4 BP and erasing LP, therefore the resulting geometry is the seesaw shape.

Let’s see now the last case and indeed the last rule too.

If the molecule has LP ≥ 2, but VP < 5, then the geometry is defined only by the position of BPs (erasing the LPs). On the other hand, if the molecule has LP ≥ 2 and VP ≥ 5, place the lone pairs in a way to minimize the lp/lp and bp/lp repulsions at 90°. The priority must be given to the lp/lp repulsions because they are the strongest ones. Finally, determine the geometry by the resulting position of BPs.

Let’s do two examples to understand point 6.

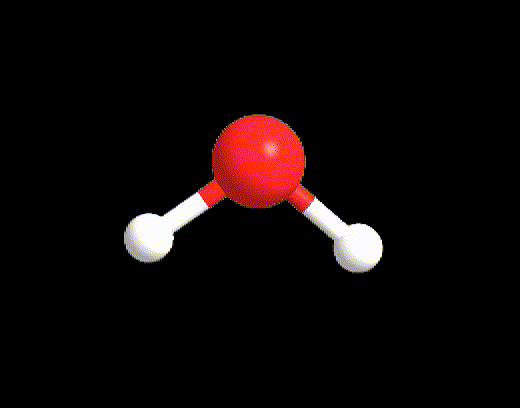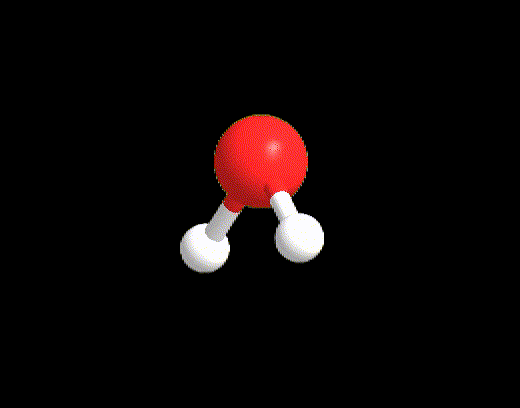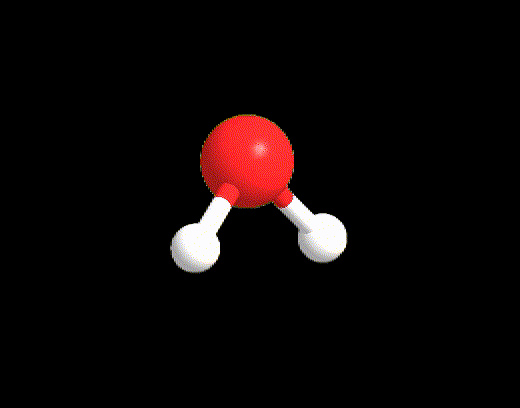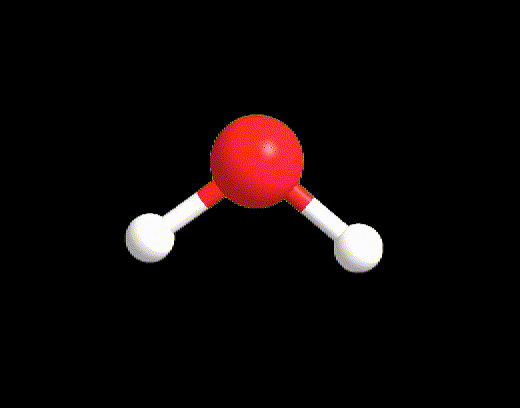
For the case LP ≥ 2 and VP < 5, an example may be the water molecule. The Lewis structure is as follows:

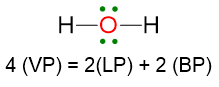
VP = 4, hence the electron disposition is tetrahedral.

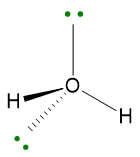
The geometry will be bent (V-shaped) because the 2 LPs must not be considered.

For the case LP ≥ 2 and VP ≥ 5, as example it may serve the ClF₃ molecule. The Lewis structure of this molecule and the number of electrons are:

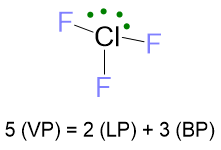
The electron disposition for VP = 5 is the trigonal bipyramid. However, there are 3 possibilities to place these 2 LPs:

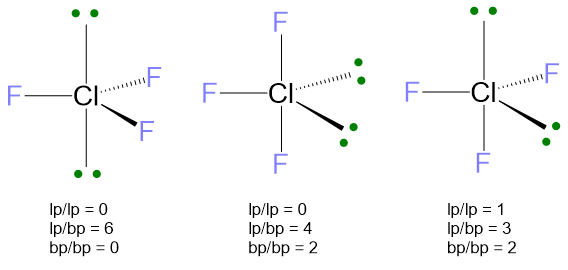
In the first structure LPs are both in axial, with an angle of 180°; in the second one, LPs are both in equatorial at 120° one far from the other; in the last structure, one LP is axial and the second one is equatorial with an angle of 90°. Comparing the repulsions lp/lp at 90°, it is evident that these lp/lp repulsions are absent in the first two structures, whereas there is one lp/lp repulsion for the last structure. Therefore, the last structure can be ruled out because the lp/lp repulsions at 90° are destabilizing on the geometry. Between the first two structures, the more stable is the second one, because it has only 4 lp/bp repulsions at 90° while the first one has 6 of them. The bp/bp repulsions, even if present in the second structure, are of least entity; this means that the 2 bp/bp repulsions, in the second structure, are not as destabilizing as the 2 additional lp/bp repulsions of the first structure.

The final molecular geometry is given by erasing the two lone pairs and the result is the T-shape.

Recapitulatory table

The following Table 2 (drag to see it enterely) summarizes all the cases you can encounter during your exercises.

Bond angles in VSEPR

As you may note from the Table above, if you compare molecules with the same VP value, the angles of the molecules with at least one LP are lower than the angles of molecules without LP.

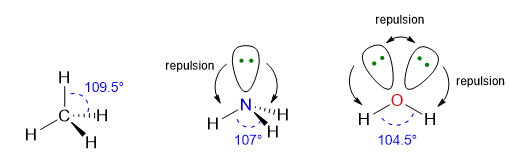
For instance, the angles of trigonal pyramid (VP = 4, LP = 1) are less than 109.5° which are the angles of perfect tetrahedral geometry (VP = 4, LP = 0). This is because each time there is a lone pair, that lone pair, which is more repulsive and takes up more space, will shrink the angles among the remaining bond pairs.

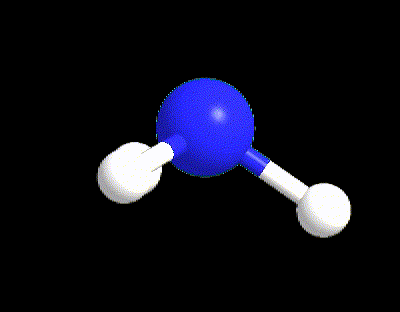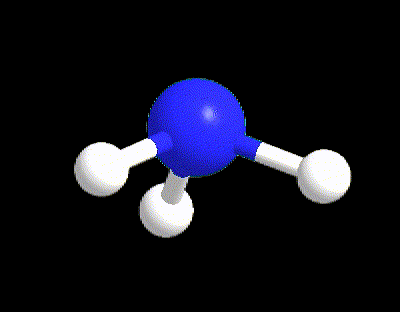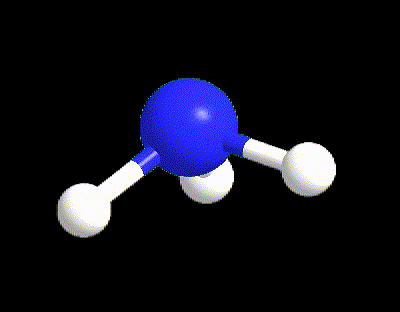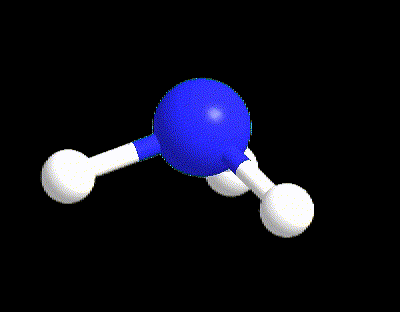
Typical examples are the molecules of CH₄, NH₃, and H₂O (Figure 6). All of those three molecules has VP = 4, however only CH₄ (LP = 0) possesses the perfect 109.5° angles of the tetrahedral electron dispositions, whereas NH₃ and H₂O have angles equal to 107° and 105° respectively. The angles in water are even more reduced because there are 2 LPs in the molecule exercising a bigger repulsion between each other and with the BPs.