Introduction
In this article, we talk about chemical kinetics, an important topic not only in general chemistry, but also in all the fields of chemistry.
In fact,,
kinetics studies the rate of chemical reactions.
This argument has many practical applications. For example, if we are an industry that has to produce a substance and sell it, we would be inclined to produce it in the shortest time as possible; therefore we would be interested in reactions that take place in a reasonable time (from a few minutes to a few days), while we would rule out reactions that are too slow (e.g. reactions that take months or years). Similarly, kinetics is also essential for researchers, because the study of kinetics provides information on the mechanism of a reaction.
In summary, chemical kinetics allows us to have information on:
- The rate of a reaction;
- The reaction mechanism.
Inaccurate definition of speed (average speed)
As in physics, speed is always the change of some property over time. Therefore, in chemistry, to define the rate of a reaction, we must identify this property that varies over time. The answer can only be concentration, since during the course of a reaction the concentration of the reagents decreases while that of the products increases. It can be written that:
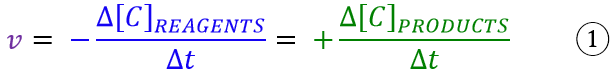
The speed is therefore the variation of the concentration of the reagents or products (Δ[C]) over the time (Δt) in which the same variation takes place. Note the minus sign when the rate is expressed with the concentration of the reagents. Without this minus sign, the rate would be negative, because the concentration of reagents decreases during the reaction. Hence, since chemists don’t like the idea of a rate with a minus sign, they opted to add another negative sign, so that the result would be positive. It is a simple convention, to be learned by heart, unfortunately!

Would you like to have this article offline, to read it comfortably and whenever you want? Download the pdf or docx file related to this article here.
Let’s take an example to understand equation 1. Suppose we have the following reaction:
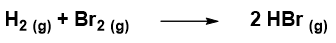
and to have calculated that in 200 s the molar concentration of Br2 decreased from 3.00 mol L-1 to 1.50 mol L -1. The consumption rate of Br2 according to 1 will be:
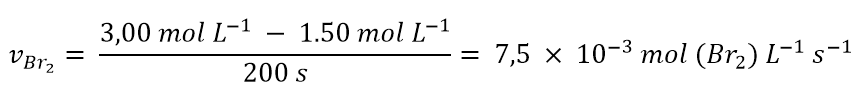
Therefore, we have seen that speed depends on concentration. Now let’s see how to write the speed for a generic reaction like:

The reaction rate will be expressed as:
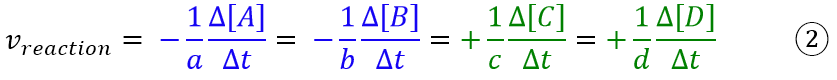
The reason for dividing by the stoichiometric coefficients is the same as in the case of weight ratios in chemical reactions, where for the same generic equation one can write the expression:
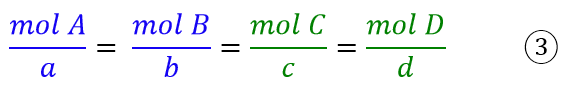
So if I want to know the moles of C formed from the moles of A, I should divide the moles of A by the stoichiometric coefficient a and then multiply the result by the coefficient c. Since the rates in chemistry depend on the concentration, which in turn depends on the moles involved, then also the rate of formation or consumption of a chemical species will depend on the stoichiometric coefficients, which will therefore have to be considered.
At this point, in order to avoid confusion, it is convenient to distinguish between:
- reaction rate which is independent of the stoichiometric coefficient and is the same for all the chemical species (equation 2);
- rate of formation/consumption with respect to a chemical species, which depends on the stoichiometric coefficients.
The following example will clarify the difference between these two speeds.
Let’s take an example to better understand equation 2. Consider the following reaction:
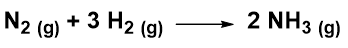
The NH3 formation rate has been reported as 1.15 mol (NH3) L-1 h-1, we have to calculate the rate as a function of H2, the rate as a function of N2, and the rate of the reaction. Using equation 2 and considering that each 2 moles of NH3, 3 moles of H2 are consumed, we obtain:
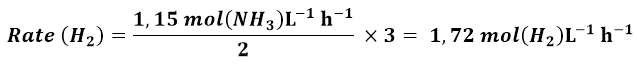
Similarly, the N2 consumption rate will be given by:
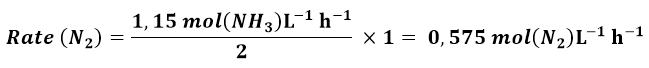
The reaction rate, according to 2, can be calculated from the NH3 formation rate divided by its stoichiometric coefficient:
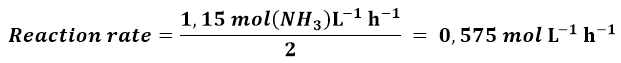
In a similar manner, I could calculate the reaction rate by dividing the N2 consumption rate by its stoichiometric coefficient and similarly if I consider the H2 consumption.
Precise definition of speed (instantaneous speed)
If we recall some basics of kinetics in physics, we can easily understand that equation 1 is valid only for speeds which are constant. However, the rates of chemical reactions are not constant, but tend to slow down as the reactants are consumed.
In fact, the typical trend of the concentration of the reagents (left, Figure 1) or of the products (right) over time can be seen in the two graphs below.
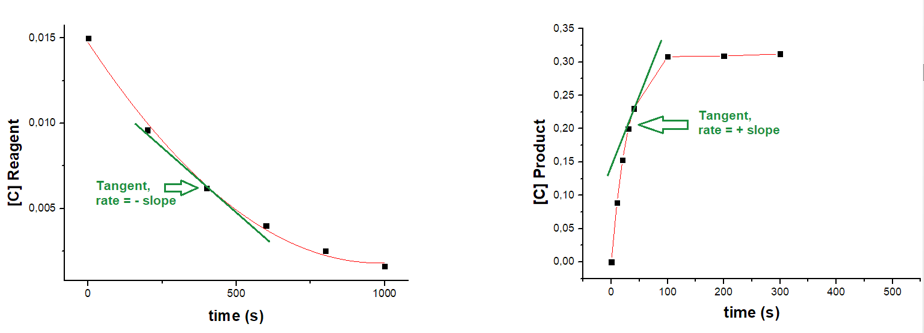
In the graph on the left, you can see how the concentration of a generic reagent decreases rapidly at first and then more and more slowly. Similarly, the concentration of products, graph on the right, increases rapidly at first and then more and more slowly.
To follow the speed trend, just draw a tangent line to the point of interest, as shown by the green line in Figure 1. The angular coefficient of this line, i.e. its slope, determines the speed at that point. In the case of reagents, the slope will be negative (the line leans to the left), while for products it will be positive (the line leans to the right).
To know the rates at all points of the curve, it will be necessary to draw a tangent for each of these points. This operation in mathematics is equivalent to the concept of first derivative. Therefore we can define the instantaneous rate of a chemical reaction as:
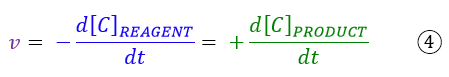
the derivative of the concentration of reagents or products with respect to time.
In the case of a generic reaction, the various speeds of the chemical species will be related to each other according to equation 5:
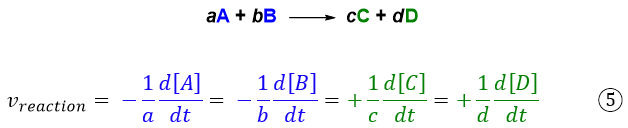
In summary, we can define the rate of a reaction as the derivative with respect to time of the concentration of one of the species taking part in the reaction divided by the appropriate stoichiometric coefficient and transformed into a positive number.
Kinetic law
Equation 5 is not of much practical use and is difficult to solve, since it is a differential equation.
So number 5 can be used as a definition of the reaction rate, but from a practical point of view, chemists use the kinetic law: an equation that can only be found experimentally, i.e. by measuring the concentrations of reactants and products over time. The kinetic law is expressed as follows:
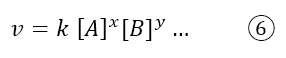
Where k is the rate constant which is independent of concentrations, but depends on temperature; [A] and [B] are the concentrations of the reactants (but the concentrations of the products can also sometimes appear) and x and y are coefficients that are found experimentally. They do not correspond to the stoichiometric coefficients of the overall reaction, but to the stoichiometric coefficients of the elementary step (topic that we will cover in the next article). The equation is written with an ellipsis because it is experimental, so one cannot know exactly how many and which reagents will affect the kinetics.
For example, the decomposition reaction of acetaldehyde is as follows:
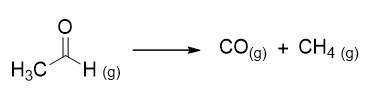
The kinetic law found experimentally is:
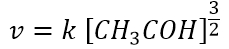
As one can see, the kinetics depends only on the concentration of the acetaldehyde; furthermore the coefficient 3/2 has nothing to do with the stoichiometric coefficient (equal to 1) of the overall balanced reaction, but it is a value to find experimentally.
Returning to the generic kinetic law (equation 6), the exponent x identifies the reaction order of the chemical species A, while y identifies the reaction order of reagent B. The overall order of reaction is given by the sum of the coefficients: x+y.
Let’s take an example. Given the following reaction:
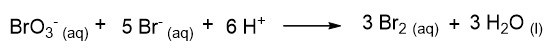
it is found experimentally that the kinetic law is:
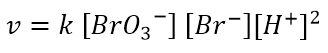
This implies that the order of reaction with respect to BrO3– and Br– is 1, while the order of reaction with respect to H+ is 2. The overall order of reaction is 4.
The order of reaction can also be a fraction, as already seen in the case of the decomposition of acetaldehyde, where the order with respect to acetaldehyde is 3/2, which also coincides with the order of reaction.
There are also reactions with zero order kinetic law; in this case, the rate is independent of the concentration of any species in solution and is constant. As an example we can use the decomposition of phosphine (PH3) on tungsten heated to high pressure, with the following kinetic law
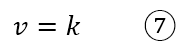
The overall order of the reaction is zero. A zero-order rate law is possible only for reactions that occur in the heterogeneous phase.
Determination of the kinetic law
How can we determine the kinetic law in practice?
There are two methods: the isolation method and the initial velocity method.
Isolation method
The first method is based on using an excess of all but one of the reactants. For example, given a generic reaction between a species A and a species B, if I put B in a strong excess, with a good approximation I will be able to consider the concentration of B constant for the whole reaction. This gives me the ability to wrap [B] in the kinetic constant and write:
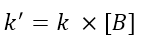
Assuming a kinetic law of the type v = k[A][B], since now the concentration of B is constant, we could rewrite the equation as follows:
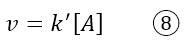
This kinetic law takes the name of pseudo-first order kinetic law, precisely because the reactant B has been deliberately made constant, modifying the real kinetic law.
With the method of isolation, the kinetic law is found by following the trend of the velocity with respect to each isolated reactant in turn, while keeping the other substances in excess. In our example we isolate A while maintaining excess B and then isolate B while maintaining excess A.
Initial rate method
Instead, the initial rate method, which is often used in conjunction with the isolation method, is applied by measuring the initial rate of the reaction with respect to different concentrations of the reactants. Returning to our generic reaction of A reacting with B, we can write that the kinetic law with respect to A is:
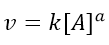
The initial velocity (v0) will therefore be given by the initial concentration of A, according to:
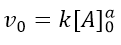
If we take logarithms, we get the equation of the straight line:
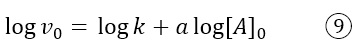
with intercept log k and slope a, the order of the reaction with respect to A. We can make a similar consideration for B.
Therefore, with this second method, the initial rates of the reaction are recorded, keeping the concentration of B constant, but varying that of A; with the values obtained the straight line is constructed according to equation 9 and the slope a is found which corresponds to the order of the reaction with respect to A. The same is done with B: the concentration of A is kept constant and the initial rate of the reaction is measured at various initial concentrations of B. The straight line is constructed according to the equation, which this time contemplates [B]:
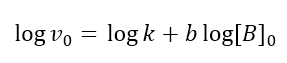
The slope of this line will give the order of reaction with respect to B.
Exercise 1
Let’s take an example. Let’s take the reaction
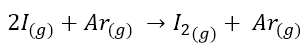
The reaction was first studied by holding the [Ar] steady and monitoring the initial rate at various initial concentrations of I, according to the data set forth in the following table.

Then [I] was kept constant and the initial velocities were measured at various initial [Ar] concentrations. The data are shown in the following table:

To determine the reaction order with respect to both species, one must plot the log of the initial rate, v0, against the log of the initial concentration of I and then construct a second graph against the initial concentration of Ar. The following lines are obtained:
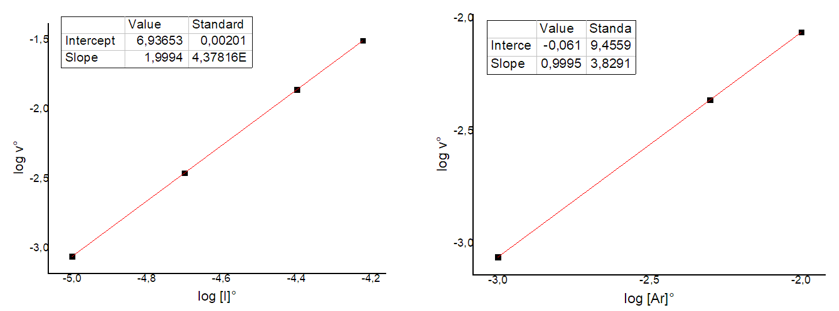
From the slope of the straight lines (see slope values in the table embedded in the graphs) the values of a and b are obtained, i.e. the reaction orders. In the case of iodine, the order of reaction is 2, while in the case of argon, the order is 1. So we can write the overall (initial) kinetic law as follows::
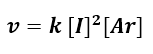
However, the initial velocity method may not be accurate if the products affect the kinetics. Therefore, after having obtained the kinetic law, we should always compare it with the experimental data relating to the concentrations of all the species involved in the reaction.
The exercise shown above, however, is not one of the typical exercises, students can encounter during chemistry exams, because most likely they will not be able to use a computer to draw the straight line and calculate its slope. Therefore, in the exam session they will face an exercise very similar to the previous one, but to be carried out in a different way. Let’s see an example below.
Exercise 2
For the generic reaction A + B + C → products the following data have been obtained:
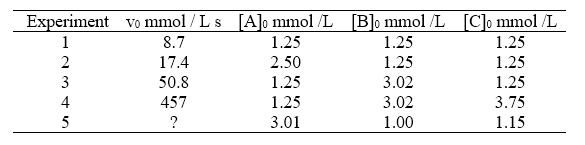
a) Formulate the kinetic law of the reaction;
b) Establish the order of the reaction;
c) Determine the kinetic constant;
d) Predict the rate of the reaction in experiment 5.
To determine the kinetic law (point a), it is first necessary to calculate the order of reaction with respect to each reactant. Let’s start with reagent A. As can be seen from the table, experiments 1 and 2 can be used for this calculation, because the initial concentrations of B and C are fixed while those of A vary. Therefore, from these two experiments I can get information on the influence of A in the kinetics by writing the equation
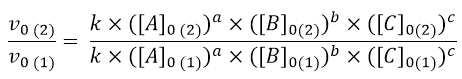
Since [B] and [C] in experiments 1 and 2 are equal, they can be eliminated, so can the constant k. Hence, the equation becomes:
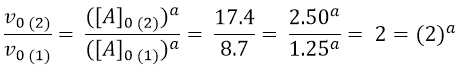
In this case it is easy to understand that the value of a is 1. We then proceed to determine the order of reaction with respect to B. For the purpose we can use experiments 1 and 3, where [B] varies, while [A] and [C] are constants.
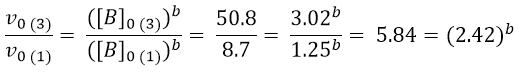
To obtain the value of b we can use logarithms:
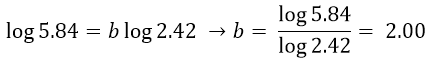
It remains to calculate the order of reaction with respect to c. This time we will compare experiments 4 and 3.
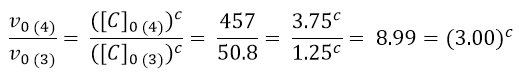
As done previously, we use logarithms to get the value of c:
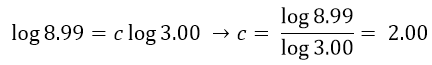
Having obtained the order of reaction with respect to each reactant, we can write the equation rate:
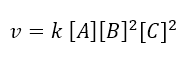
The overall order of the reaction (point b of the exercise) is given by the sum of the orders of reaction of each chemical species determining the kinetics; so the reaction order is a + b + c = 1 + 2 + 2 = 5.
To calculate the kinetic constant (point c), just take some of the data in the table, insert them into the kinetic equation obtained and obtain k. For example, let’s take the data relating to experiment 1, we will have:
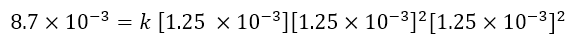
From which k is easily obtained
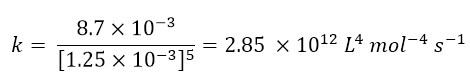
Finally, to determine the rate of the reaction in experiment 5 (question d), it will sufficient to insert all the data of experiment 5 and the kinetic constant within the kinetic law:
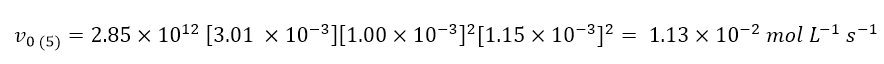
This lesson

Kinetics
€
1.00
Download as pdf (unchageable) file

Kinetics
€
2.00
Downoald as docx (editable) file

