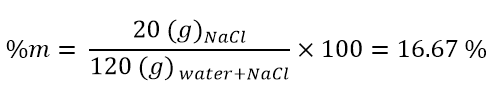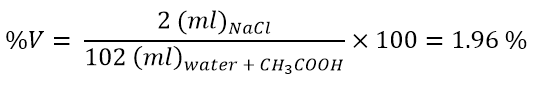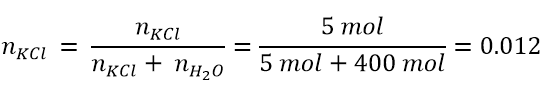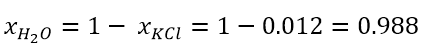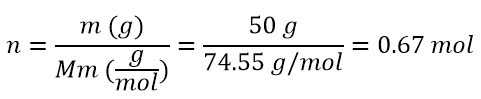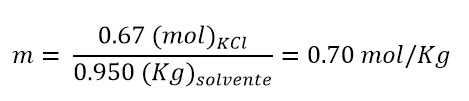Definition
What is a solution?
A solution is a HOMOGENEOUS mixture made up of at least two components: SOLUTE and SOLVENT.
The coloured words are very important to understand the definition of solution. Let’s start with the word HOMOGENEOUS. To understand what this means, consider the following examples:
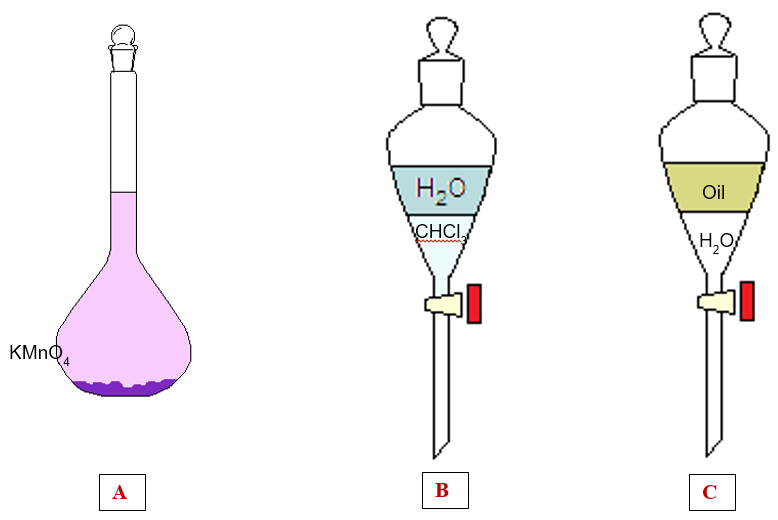
Of the three situations above, none represents a solution. In fact the figure:
– A represents a mixture of water and potassium permanganate, KMnO4, purple solid. However, this is not a solution because it is not homogeneous, in fact part of the solid KMnO4 remained deposited on the bottom. It’s actually a saturated solution, a concept we’ll cover in a future article.
– B represents two layers formed by two immiscible substances: water and chloroform. This is also not a solution because we can distinguish two layers that don’t mix, so it’s not a homogeneous mixture.
– C is very similar to the previous case, only this time the two immiscible liquids are oil and water. This is not a solution too because it is not homogeneous.
We finally see a case of true solution in the following image:
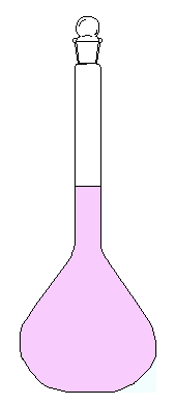
This is a SOLUTION of water and permanganate. Situation very similar to case A, only this time we put much less KMnO4, so that it was all solubilized in water. Therefore the mixture is finally HOMOGENEOUS because we no longer distinguish the solvent (water) from the solute (potassium permanganate), which has ”disappeared” in the water.
Therefore, we now understand the first part of the definition. However, what does it mean: made up of at least two components: SOLUTE and SOLVENT?
The phrase refers to the fact that a solution can also be composed of several solutes (e.g. NaCl and NaOH, both solid) dissolved in a solvent (e.g. water); however, in order to be able to speak of a solution, it is enough that there are at least the two main components SOLVENT and SOLUTE.
The solvent is generally the substance present in excess, while the solute is the one present in defect. The solute does not have to be a solid, but it can also be a liquid or a gas miscible with the solvent. Similarly the solvent can be solid (like iron in steel), liquid or gaseous (like nitrogen in air).
Would you like to read this article offline? You can download the pdf or docx file here.
Types of solutions
Solutions are divided into two large classes: non-electrolytic solution and electrolytic solution.
- A non-electrolyte solution is a solution that is unable to conduct electricity. An example is water and sugar, where the sugar molecules dissolve in water, giving rise to neutral molecules.
- An electrolytic solution is a solution capable of conducting electricity, this is because in solution the solute splits into ions, charged particles. An example is NaCl in water. This salt not only dissolves in water, but also disintegrates into Na+ and Cl– ions, charged particles..
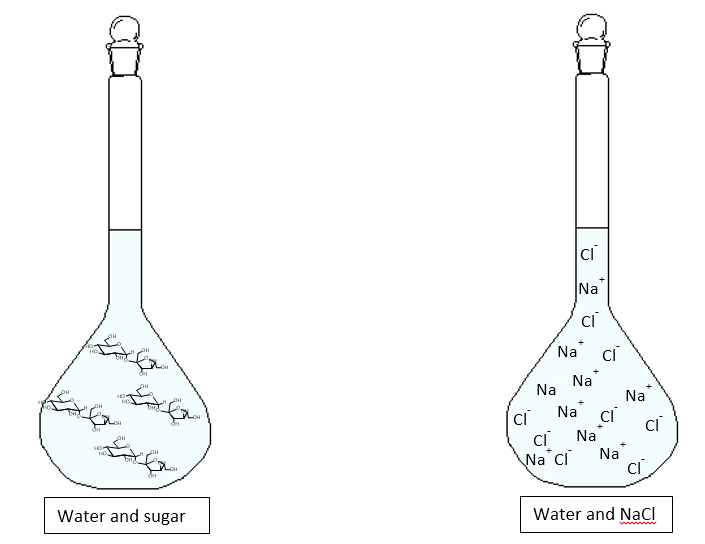
However, the electrolyte solution is divided into two other categories (strong electrolyte solution and weak electrolyte solution), let’s see what they are.
- A strong electrolyte solution is a solution in which the solute (electrolyte) completely dissolves into its ions. An example is again NaCl in water; sodium chloride, in fact, completely disintegrates into the Na+ and Cl– ions without any NaCl being left in solution. Â
- A weak electrolyte solution is a solution in which the solute (the electrolyte) does not completely dissolve into its ions, but remains partially undisintegrated. An example is acetic acid, CH3COOH, which partly splits into its CH3COO– and H+ ions, and partly remains CH3COOH.
Solution composition
The composition of a solution refers to the quantitative aspect of a solution, therefore to the concept of CONCENTRATION. Concentration is a way to define quantitatively the solution, making clear how much solvent and how much solute the solution contains.
There are various ways of expressing concentration, depending on the physical quantities used. The quantities are as follows:
– mass and volume, known as physical quantities;
– moles and equivalents, known as chemical quantities.
Therefore, there are concentrations expressed with physical units only, those expressed with chemical units and finally those expressed with both. Let’s see them in detail in the following paragraph.
Concentrations in physical units
Percentage by mass
Using the physical quantity mass, we can define the first concentration: the percentage by mass. This concentration is expressed as follows:
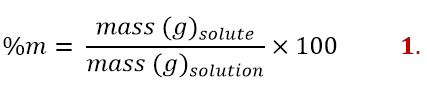
Therefore, it is the ratio between the mass of the solute and that of the solution multiplied by 100. Being a ratio between equal quantities (both are masses), this concentration is independent of units of measurement. For example, I could use both masses in kilograms (kg) or both in grams (g) and the result would be the same. The important thing is to report both masses with the same unit of measurement; to be clear, it would be a mistake to write the mass of the solute in grams (g) and that of the solution in kilograms (kg).
This type of concentration is usually used when the solute is solid.
Do this short exercise to check your comprehension about mass percent:
- A solution was prepared by dissolving 20 g of NaCl in 100 g of water. What will be the mass percentage of this solution?
Just put numbers in the right position of equation 1, as below::
As you can see above, the calculation was carried out by placing the mass of the solute (NaCl) in the numerator and the mass of the solution in the denominator. However, the mass of solution is given by the mass of the solute (20 g) + the mass of the solvent (100 g). Then everything is multiplied by 100.
Percentage by volume
Volume percent is very similar to the previous concentration, but instead of using masses, use volumes.
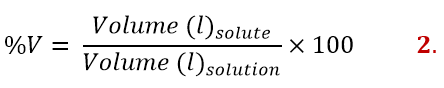
This type of concentration is usually used when the solute is liquid.
Do this exercise to see if you understand:
- We have prepared a solution by adding 2 ml of acetic acid to 100 ml of water. Calculate the concentration in percent by volume.
Similarly to the previous concentration, the result will be given by
Mass/volume percent
The mass/volume percent comes from the combination of the previous two ones and is expressed as follows:
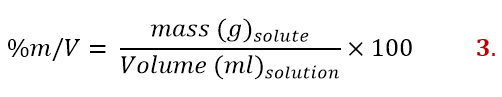
This way to express concentration is mostly used with saline solutions.
It is important here to pay more attention to the units of measurement, since the same proportion must be maintained. For example if I use grams (g) for mass, I must use millilitres for solution; similarly if I use kilograms for the mass, I must use litres for the volume of the solution. And so on.
Grams over litre
The grams over litre concentration is expressed as the mass of solute (g) over the volume of solution in litres (l):
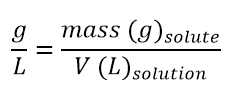
This concentration is actually a variant of the previous one; in fact the ratios between the units of measurement have changed: no longer [g]/[ml] but [g]/[l].
Concentrations in Chemical units
Mole fraction
The mole fraction can be expressed for each component of the solution. For example, there will be a mole fraction of the solute and one of the solvent. The mole fraction of the solute is the ratio between the moles of the solute and those of the solution, according to:
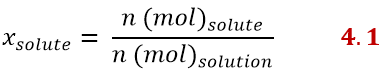
While the mole fraction of the solvent is expressed similarly as:
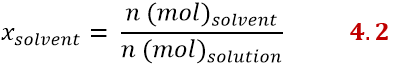
Since the molar fractions, as the word itself suggests, are fractions, we can obtain the molar fraction of the solvent, knowing that of the solute and vice versa as follows:
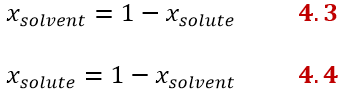
If the solution contains more than one solute there will be a mole fraction for each component of the solution, so the generic equation would be:
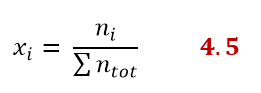
Do the following exercise to test your understanding:
- Suppose we have a solution formed by 5 mol of KCl in 400 mol of water; what will be the mole fraction of KCl and which of the solvent?
Just use equation 4.1 to calculate the mole fraction of the solute:
That of the solvent is quickly obtained by applying 4.3:
Concentrations in Physical and Chemical Units
Molality
Molality (m) is defined as the ratio of moles of solute to the mass of solvent expressed in kilograms
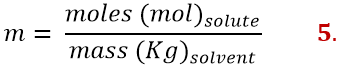
Questa concentrazione si distingue da tutte le altre perché è l’unica ad avere una proprietà del solvente (la massa) al denominatore, mentre tutte le altre hanno al denominatore sempre e solo una proprietà della soluzione.
Per questa concentrazione, come per le altre a seguire, è importante ricordare le unità di misura con cui esprimere le moli e la massa, che sono rispettivamente mol e chilogrammi. Variazioni delle unità suddette, senza mantenere la stessa proporzione, comporteranno necessariamente un errore e forse anche una sonora bocciatura. Perciò basterà ricordarsi di esprimere la molarità come [mol]/[Kg].
Molality is a concentration that does not vary with temperature, so it can be used in all those experiments where the solutions are subject to sudden changes in temperature.
Do this exercise to test your understanding:
- If we have 950 g of water in which 50 g of KCl are solubilized, what will be the molality of the solution?
First we have to calculate the moles of solute, using the molar mass of KCl which is 74.55 g/mol :
Now we can calculate the molality according to equation 5, taking care to convert grams to kilograms:
Molarity
Although its name is very similar to the previous concentration, the molarity is actually expressed differently. It is in fact the ratio between the moles of the solute and the volume of the solution expressed in litres. The units of measurement are indeed [mol]/[L].
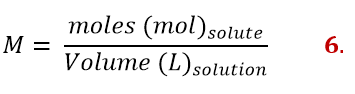
To better understand molarity, let’s imagine that we have to prepare a 1M solution of NaHCO3 in water. How to proceed?
Actually, 1 M means 1 mol of solute, NaHCO3, in one litre of solution. Therefore, it will be enough to weigh a mole of NaHCO3, after converting the moles to mass as follows:
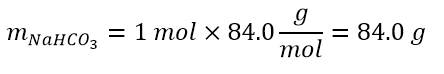
Therefore, 84.0 g will be placed in a volumetric flask, which is an instrument suitable for preparing molar solutions and which bears a notch to indicate a precise volume (see image below). So in our example we will take a 1L volumetric flask, in order to be sure of having one litre when the notch is reached. After inserting our solute (84 g), we insert part of the solvent, but without reaching the notch yet. We shake the flask a little to solubilize all the solute. Once the solution is clear and without solid residues, we can add the rest of the solvent up to the notch.
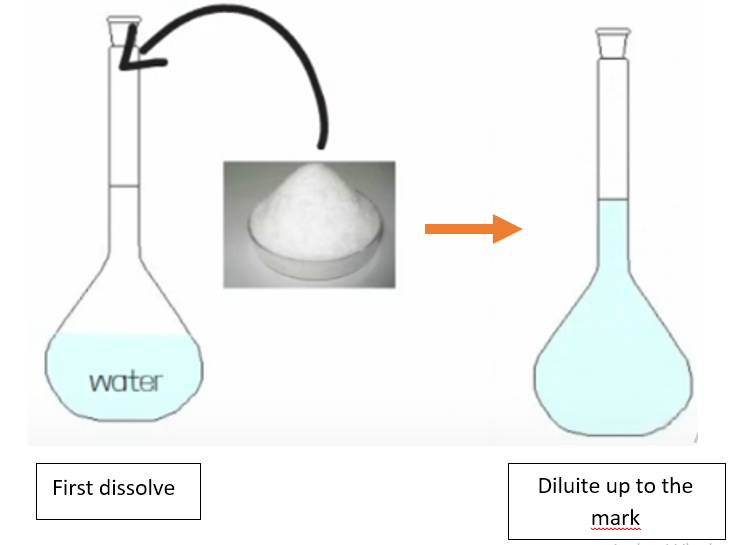
The reason why the dilution up to the mark is done last, is that the solubilisation of a solute in a solvent involves an increase or decrease in volume, depending on the type of solvent/solute interaction. So, going back to our example, if we directly add 1L of water and then insert the solute, at the moment of solubilisation the volume could increase and the solution would not exactly be 1L.
Normality
Normality is very similar to molarity, but instead of using moles, use equivalents. It is expressed as:
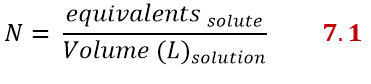
There is a relationship between molarity and normality and it is the following:
Where v is an integer, so v = 1,2,3,4…. This implies that molarity and normality are equal if v = 1, otherwise the normality is usually greater. The number v refers to the number of charges (for reactions between ions) or the number of electrons (for redox reactions) of the balanced reaction.
To better understand, let’s take an example. Let’s take the dissociation of hydrochloric acid in water, the balanced reaction is as follows:
v in this case is 1, because a positive (+1) and a negative (-1) charge has developed to the left of the equation. In this case N = M.
Instead, if we consider the dissociation of iron sulphate, the balanced reaction is as follows:
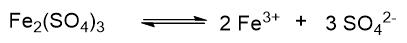
here v = 6, because on the left there are two 3+ charged iron ions, for a total of 6+, and three 2- charged sulfate ions, for a total of 6-. In this case N = M × 6.
Having clarified what v is, we can finally define the equivalents as the ratio of mass to equivalent mass. The equivalent mass is obtained by dividing the molar mass by v:
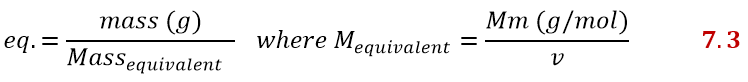
If you don’t like this equation, there is another one that comes from the previous one, but easier to remember. Equivalents can also be calculated as the product of moles and v:
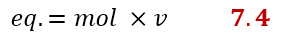
Let’s take an example to calculate normality. Suppose we have 1 g of Fe2(SO4)3 and we dissolve it in a 1L volumetric flask. After adding the solvent up to the mark, we wonder what the normality of such a solution is. We already know from the reaction written above that v = 6, so we can easily calculate the equivalents as follows:
Since the normality is the ratio of equivalents to the volume of the solution and since the final volume is 1 L, then 0.015 is also the normality value.
This lesson
Solutions & Concentrations
€
1.50
Download as pdf (unchageable) file
Solutions & Concentrations
€
2.50
Downoald as docx (editable) file